L’hydrodynamique s’intéresse aux fluides en mouvement dans une conduite (tuyaux,…) et permet de calculer les différents paramètres physiques de ces fluides (pression, volume, masse, vitesse,….).
Notion de débit
Le débit est le quotient de la quantité de fluide qui traverse une section droite de la conduite par la durée de cet écoulement.
On distingue 2 types de débit : le débit massique (unité : kg·s-1) et le débit volumique (unité : m3·s-1).
Si Δm est la masse de fluide qui a traversé une section droite de la conduite pendant le temps Δt, par définition le débit-massique est :
Si ΔV est le volume de fluide qui a traversé une section droite de la conduite pendant le temps Δt, par définition le débit-volume est :
La masse volumique ρ est donnée par la relation :
![]() d'où :
d'où : ![]()
Expression du débit en fonction de la vitesse v
Le débit-volumique s’exprime en fonction de la vitesse du fluide s’exprime par la relation :
![]()
Avec v = vitesse moyenne du fluide en m.s-1 ; S = surface de la section de la conduite en m².
En général la vitesse v n'est pas constante sur la section S d'un tube de courant ; on dit qu'il existe un profil de vitesse (à cause des forces de frottement).
Équation de conservation de la masse ou équation de continuité
Considérons un tube de courant entre deux sections S1 et S2. Pendant l'intervalle de temps Δt, infiniment petit, la masse Δm1 de fluide ayant traversé la section S1 est la même que la masse Δm2 ayant traversé la section S2.
![]() et donc
et donc ![]() que l’on peut écrire
que l’on peut écrire ![]()
Un convergent est composé d’un tuyau conique de longueur l reliant une canalisation amont de rayon R1 = 50 mm et une canalisation aval de rayon R2 = 25 mm.
Le fluide utilisé est de l’eau (ρ= 1000 kg.m-3) et le débit volumique vaut QV = 30 m3.h-1
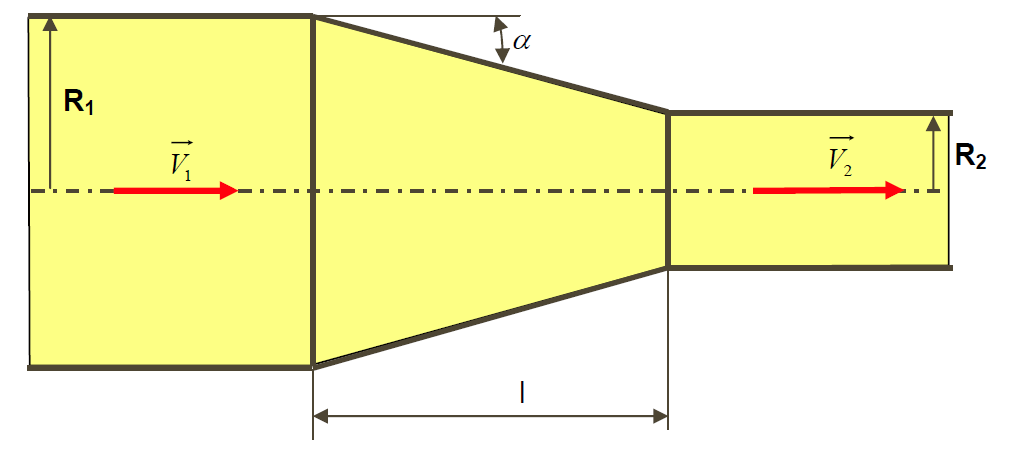
.s-1
v1 est multipliée par 4 ; v2/v1 = S1/s2 = (R1/R2)² = (50/
Un fluide parfait est un fluide dont l'écoulement se fait sans frottement.
On considère un écoulement permanent d’un fluide parfait, entre les sections S1 et S2, entre lesquelles il n’y a aucune machine hydraulique, (pas de pompe, ni de turbine).
Les caractéristiques du fluide en mouvement sont sa pression p, sa vitesse v, et son altitude z.
Le théorème de Bernoulli s’écrit :
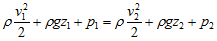
Dans cette relation, chaque terme est exprimé en pascal.
On peut exprimer la même relation en divisant tous les termes par ρg, ainsi la pression est exprimée en mètres de colonne de fluide.

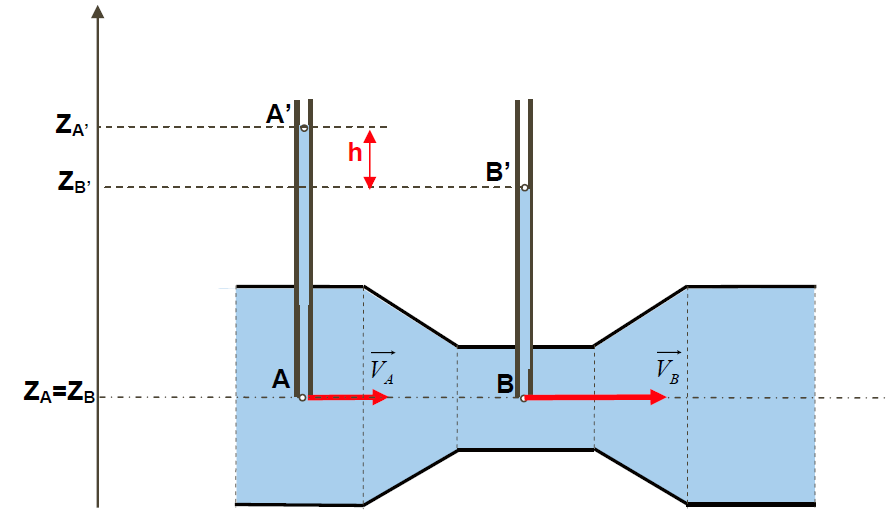
Un tube de Venturi est constitué d’un rétrécissement dans une conduite. Deux prises de pression en A et B permettent de mesurer le débit dans la conduite.
On donne :
Fluide utilisé : eau de masse volumique ρ = 1000 kg/m3
Diamètre de la conduite en A : DA = 50 mm
Diamètre de la conduite en B : DB = 20 mm
Hauteur h = ZA’ – ZB’ = 10 mm
Pression atmosphérique en A’ et en B’
Accélération de la pesanteur g = 9,81 m/s²
4 ≈ 
On s’intéresse au cas général d’un écoulement réel dans lequel on interpose une machine hydraulique (pompe ou turbine ) qui va échanger de l’énergie avec le fluide et en tenant compte des pertes de charges par frottement du fluide sur les parois de la conduite et par accidents de parcours (coudes, changement de diamètre , …)
Le théorème de Bernoulli s’écrit alors :
![]()
où tous les termes sont exprimés en pascals
P >0 si le fluide reçoit de l'énergie de la machine (pompe),
P <0 si le fluide fournit de l'énergie à la machine (turbine),
P = 0 s'il n'y a pas de machine entre (1) et (2).
Remarque : on peut écrire le même théorème en divisant tous les termes par ρ.g auquel cas les différents termes seront exprimés en mètres de colonne de fluide. Si on divise par ρ, les termes sont exprimés en J/kg.
Un fluide réel, en mouvement, subit des pertes d'énergie dues aux frottements sur les parois de la canalisation (pertes de charge systématiques) ou sur les "accidents" de parcours (pertes de charge singulières). Les paramètres influents sur les pertes de charges sont généralement le débit, la masse volumique, la viscosité, la rugosité et la section des conduites.
Suivant l’écriture de du théorème de Bernoulli, on utilise les pertes de charges en pascals, en mètres de colonne de fluide ou en J/kg.
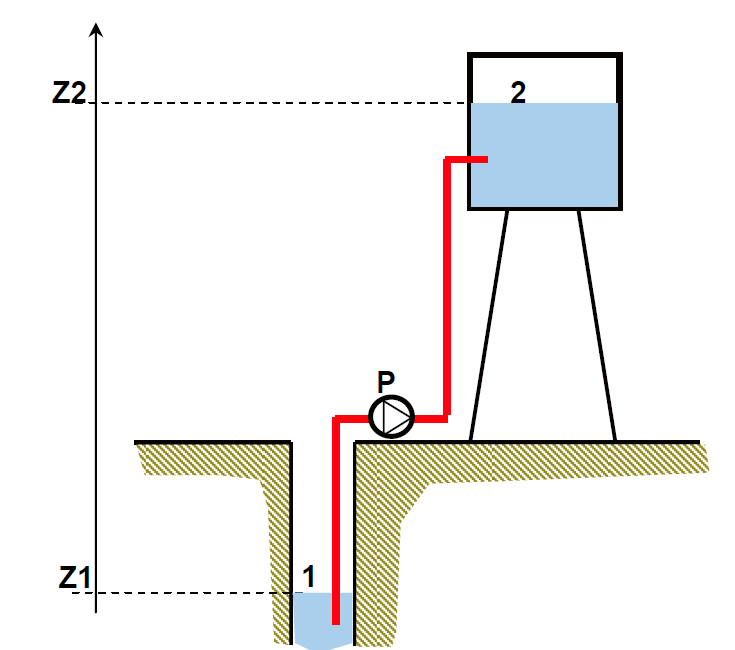
Une pompe P alimente un château d’eau à partir d’un puits au travers d’une conduite de diamètre D=150 mm
On donne les altitudes Z1=-5 m ; Z2= +26 m.
La pression en 1 et 2 est égale à 1,013 bar.
La vitesse moyenne de l’eau est v=0,4 m/s
Les pertes de charges entre 1 et 2 sont estimées égales à J1-2 = – 1 J/kg
Qv= v. S = v.π.D²/4 = 0,4 × π × 0,15² / 4 ≈ 0,007 m3/s
Même diamètre de conduite en 1 et 2 donc les vitesses sont égales
Equation de Bernoulli en J/kg :
0 + 9,81 (26+5) + 0 = 
Pu ≈ 2135,8 W
Créé avec HelpNDoc Personal Edition: Créer des documents d'aide HTML facilement